前言：

这篇文章主要是用来给大家讲解一些知识点什么的，我主要会根据老师平时布置的题目来讲述一些平时的知识点，希望各位可以从中学习到东西。同时希望大家注意的是，这个文章并不会讲的很详细，就是不会像课本一样告诉你一些详细的底层公式，所以大家还是要好好学习课本里的知识。

第一章：质点运动学

基本公式回顾

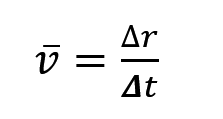
首先我们要分清两个东西，一个是平均速度，一个是平均速率，首先怎么定义平均二字，有除时间的不就是平均的吗。那什么是速度，位移 r 除以时间 t 就是速度

有很多人会把平均速度和速度的平均进行混淆，这里一并列出来

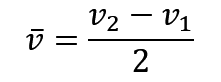
速度的平均求的是速度这个物理量的平均值，而平均速度指的是位移和时间比

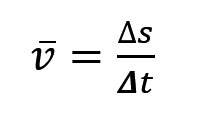
那什么又是速率呢，就是路程 s 除以时间 t。

在知道了平均这个概念后，我们再来讲讲什么是瞬时，这也很简单，你时间趋近于零时，不就相当于一瞬间的事情吗，这个时候就有了一个新的公式叫做瞬时速度公式。

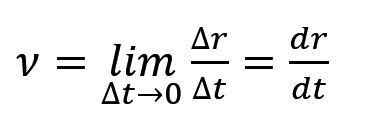
有发现吗，瞬时速度的公式只不过是让平均速度的时间趋近于零罢了。当 t 趋近于零时，那它就会等于位移公式 r(t) 的导数 ，所以这个时候，我们的瞬时速度也就诞生了。

那怎么应用呢？如果题目给你了一个位移公式 r(t)，并让你求某一时刻 t 的瞬时速度的时候，不要犹豫，直接求导带入t，那就是它的瞬时速度。如果题目给了你两个时间 t1 和 t2 ，t1<t2, 让你求平均速度，不要犹豫，先把 t2 带入，再把 t1 带入，除以 t2 – t1。

有的人很懵逼就是没看出区别，瞬时速度就是要你对 r(t) 求导，然后直接代入，不用除以时间；平均速度不用求导，代入两个时间，再除以时间的差值就行。

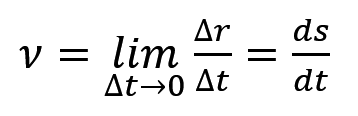
这个区别和上面的一眼给，就不多说了

接下来介绍平均加速度公式

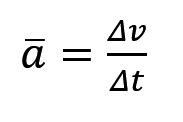
有了上面的经验，相信不用再向大家介绍平均和瞬时的区别。那什么是加速度，说人话就是速度在一定时间内的变化情况

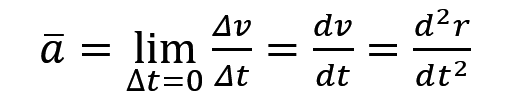
这个瞬时加速度就是平均加速度在时间 t 趋近于零时的公式，同时，这就会等于瞬时速度公式 v(t) 的导数，等于位移公式 r(t) 公式的二次导。

其实呢，理解起来没那么麻烦，如果题目给了你一个位移公式 r(t) 对不对，这个时候如果让你求瞬时加速度，你要怎么办，直接连续求导两次啊，求导一次得到瞬时速度 v(t) 公式，再求导一次得到瞬时加速度 a(t) 公式。ok，已经讲得很明白了。

直角坐标系的运用

这个坐标系其实就是为了描述物体在不同方向上的运动罢了

r=xi+yj+zk 矢量式

当你一个物体单项运动的时候，你也就没必要用上什么 i ，j，k，直接计算就行了，如果一个物体它既有水平方向位移，又有竖直方向位移的时候，我们就要用到矢量式。其中 x 表示沿着 x 轴的位移，y 表示沿着 y 轴的位移，z 表示沿着 z 轴的位移

例题讲解

已知质点在直角坐标系 Oxy 中作平面运动，其运动方程为

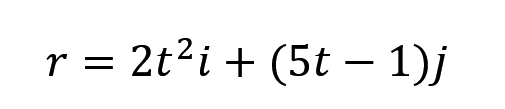
求：（1）质点从 t1 = 1 s 到 t2 = 2 s 时间内的位移；（2）质点在 t = 2 s 时的速度和加速度；

（1）好的拿到一道题目，先看看问题问了什么，这道题要我们求位移，ok，题目给了位移公式，那我们就来研究一下这个公式。

首先这个公式使用了矢量式，这说明啥，这说明这玩意在 x 轴和 y 轴上都有运动，ok，如果我们拆开来看就是两个·公式罢了

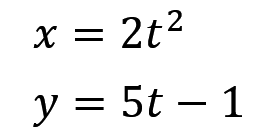
问两个时间内的位移，那就是分别把 t1 和 t2 代入然后相减

r2 = 8 i + 9 j

r1 = 2 i + 4 j

r2 – r1 = 6 i + 5 j 这个就是位移，直接写就行了，不用迟疑

如果问你位移的大小呢

那也很简单，x=6，y=5；直接勾股定理，得到 r =7.81

（2）好的来到第二题，这道题几乎贯穿了我们今天讲到的所有知识点

首先看题目，题目要我们求t = 2 s 时的速度和加速度，有什么，有一个时刻对吧，那一个时刻的速度和加速度，就是要我们求瞬时速度和瞬时加速度。

好的分析的很透彻了，我们直接做题目，瞬时速度等于什么，等于位移公式的导数，我们直接求导

v(t) = 4t i+5 j

那瞬时加速度相信你也一定会了。没错，再导一次

a(t) = 4 i

很好，这时候，你直接把 t=2 s代入即可得到答案

说了那么多，过来实战两把看看实力

答案：B；

再来一道填空题，快乐加倍

答案：

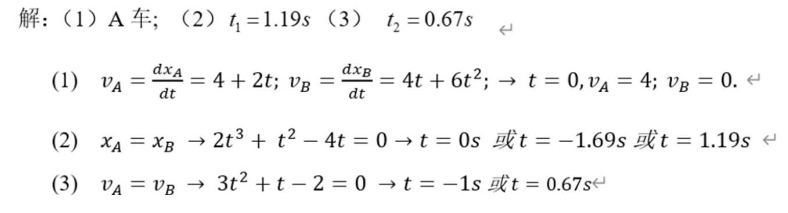
不会吧不会吧，不会有没算过看了答案就觉得自己会了的人吧

事不过三，保证这是最后一题了嘿嘿

答案：