前言

今天要讲的的东西是自然坐标系下的速度和加速度，那么今天的重点其实不在于理解多少，而是在于，该背的公式你能背熟了就行。

自然坐标系公式速通

首先我们要理解的第一个东西是，自然坐标系，其实跟直角坐标系没什么很大的不同，就是沿轨道的任意一点作一条切线和一条法线，本质上，他就类似于一个会转的直角坐标系罢了。

什么时候用自然坐标系呢，也很简单，当物体做什么s型的或者是什么乱七八糟型的曲线的时候，就会用到这玩意，但是一定要注意，我们研究的自然坐标系，仅仅只是在平面内运动，因此只有两个轴。

那么我们先来了解自然坐标系的两个轴，一个是切线方向轴

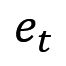
另一个是法线方向轴，并且法线的方向指向曲线凹处。

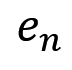
自然坐标系比直角坐标系多出来了这两个东西，就没了。了解了这两个东西后，我们直接开始速通公式

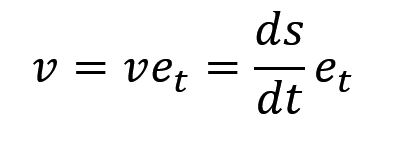
又到了我们最最最经典的速度公式，位移公式就不说了，反正就是 s(t) 嘛。这个时候大家肯定就会直接梭哈出速度公式，没错就是直接对位移公式求导。但是很显然，这次的速度公式跟以前的不同了，多了个什么，多了个速度方向呗，你直角坐标系有 x 和 y，那我自然坐标系多个 et 是不是也很正常。（要是不理解，你就直接想，速度多乘个方向，背就完事了铁汁），那这时候肯定就有人问了，哎呀，这个自然坐标系两个方向，凭啥就是 et 啊，因为 et 在自然坐标系中是切线方向，而速度肯定是沿着轨迹的切线走的，所以我们乘 et，那么，法向的 en用来做什么的呢，当然是加速度啊（老高中知识了，不会的话回炉吧）

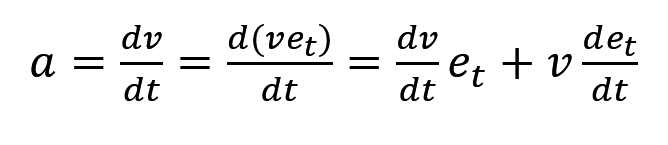
好的，映入眼帘的，是个又臭又长的公式，那么很遗憾地告诉各位，上面的不用背。只要你会导，你就肯定能出来，所以不用特地去记。

首先第一个公式，加速度公式，很简单，直接速度求导就行，多加了个 et 求导，不用管，导下去就行。

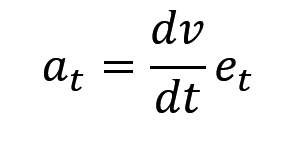
导出来是两个看不懂的东西相加，我们拆开来分析，一个为 at，一个是为an，

那么我们先来看 at ，什么东西？切向加速度，速度的变化率，好的你要听不懂没事，直接认真观察一下，这个东西是不是就是速度求导乘个 et方向，那是不是其实就是个加速度，那是不是其实就是速度大小的变化率？ok，讲的很明白了。总结来说，切向加速度就是速度直接求导。

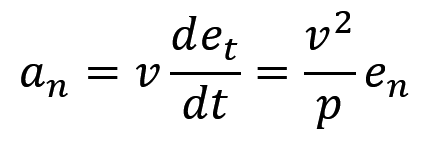
再来看看什么是 an，法向加速度，速度方向的变化率。其实理解起来也很简单，一个和你速度方向垂直的加速度，没了。一个加速度，垂直于你的速度方向，速度大小不变，方向改变（又是一个老高中知识，背就完事了）其实看到后面那个公式的时候，你也会想到一个东西叫做，向心加速度，这两个东西本质上是一样的，你要想记住，你就想着向心加速度乘个方向 en，这个时候你应该就可以理解为什么要乘 en了，因为向心加速度一直垂直于速度，那就是说，向心加速度一定在法向上，所以乘 en。

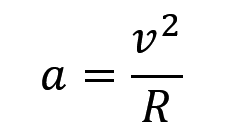
两个加速度，刚好对应自然坐标系的两个轴。合起来就是完整的加速度，如果题目问你自然坐标系下加速度的大小，那就直接勾股定理

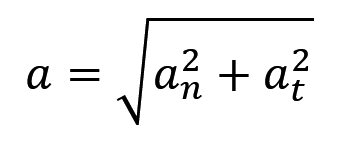
补充：额，因为这是一个月前写的，感觉略显稚嫩哈，再补充几点。首先你是自然坐标系的话，通常公式会带 i ，j ，k 三个符号，例如

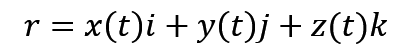
这个公式其实就是你要拆开来看，可以看成物体在 x 轴 y 轴 z 轴上的位移公式

圆周运动公式速通

圆周运动其实也没有什么特别的，如果要问加速度的话，跟上面是一样的，直接求就可以了。那在圆周运动中，会多一个公式，就是角位置公式。

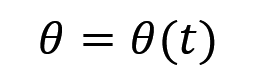
这个公式反映了角度的变化，当我们知道了角位置公式以后，直接对这个公式求导，就可以得到角速度公式

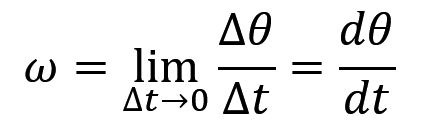
从上面看出，求角速度的规则跟上面求速度的规则是一样的，只是求导对象换成了角位置公式而已

那我们就可以推出角加速度的公式，就是角速度直接求导

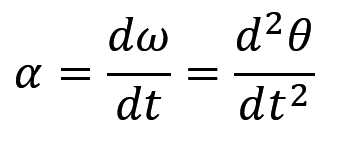
上面就已经是圆周运动最基础的公式了，但是知道这些公式往往还不够，还需要知道一些圆周运动独有的公式

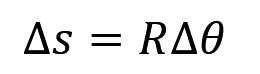
弧长公式，这个公式使用的地方在于什么，如果我们知道了半径 R，还知道了走过的角度，就可以求出位移，求出位移那我们接下来不管是速度还是加速度就都能求了；还有一种是知道了位移和半径，就可以求出角度公式，那我们反手就能求出角速度和角加速度。很实用的一个公式。

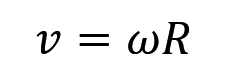
这个没什么好说的，速度和角速度之间的转化公式

接下来讲的是两个比较新一点的公式，就是切向加速度和法向加速度公式，这个也得记就是了，如果题目要考你这两个东西的话，就直接套公式算就完事了

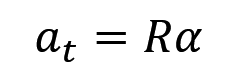
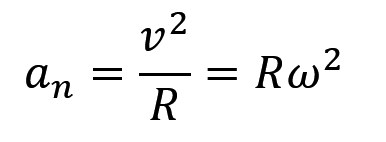
切向加速度，角速度乘角加速度

法向加速度，就是向心加速度，这个每个人应该都会

例题分析

我们来看一道课本内的经典例题。拿到一道题目，我们先分析，物体在做什么运动，然后题目要我们求什么，给了哪些参数。

首先，这道题目中的物体做圆周运动，说明会用到圆周运动的相关公式，其次，题目要我们求任意时刻的速度、加速度、角速度和角加速度。然后给了个路程时间公式 S(t) ，还已知一个半径R。

很好有个 s(t) ，我们直接求导，马上就能得到速度 v(t)，再求导又能得到加速度 a(t)，ok，如果这个时候你还接着往下做的话，你就包错的老弟，我们从上面的公式速通中可以知道，在圆周运动中，对速度直接求导，只能得到切向加速度 at，但是我们同时还得求它的法向加速度 an，求出来之后，根据勾股定理，就能得到加速度的大小。

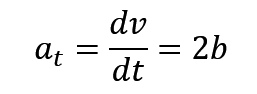
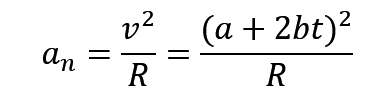
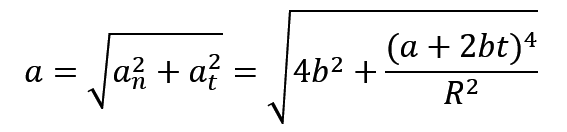
角速度的话，就要用到 v除以R的公式

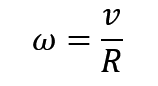
角加速度也是直接套公式

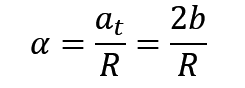
知道你可能觉得简单，但是，有难度的题目，都只是各种基础题目的叠加罢了，因此研究一道基本的题目，是一件很重要的事情。

练习

来吧什么都别说了，莽就完事了

答案

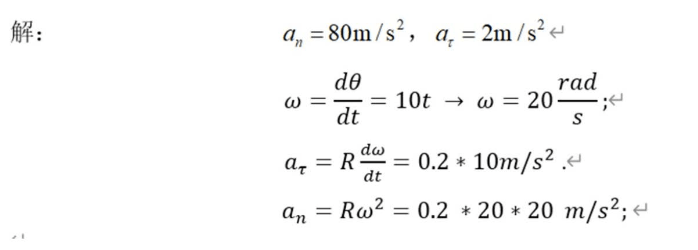
别急，再来一题，好事成双

答案：

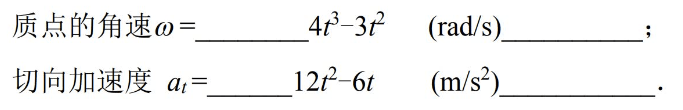
套公式的老套题型罢了，自个儿算吧

总结

本章节讲了自然坐标系下的运动以及圆周运动，公式很多，但理解起来并不困难，合理理解以后，方能更好地运用公式。