期中复习篇

基础知识一：点乘与叉乘之间的区别概括

如果用图像来表示的话，所谓点乘，可以概括为两个向量在同一水平线上的叠加。

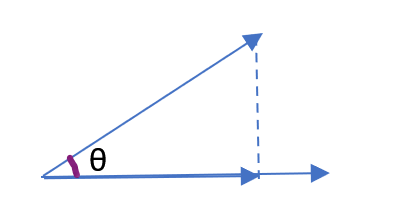
如图上两个向量，如果是点乘，那最后会变成同一水平线上相乘。因此才会有这个式子

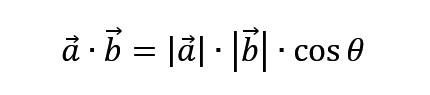
而所谓的叉乘，可以看作是求的是两个向量之间的面积。

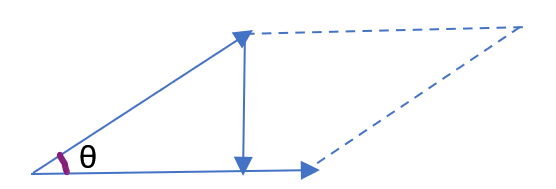
如图上两个向量，如果是叉乘，那最后会变成相当于在求这一块平行四边形的面积，因此才会有以下公式

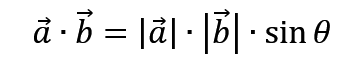
如果你觉得理解起来很麻烦，那你就，直接点乘余弦，叉乘正弦地记也可以。

基础知识二：矢量与标量全概括

矢量

加速度，速度，位移；力，力矩，角动量；角加速度，角速度，角位移；动量，冲量；电场强度，磁感应强度。

标量

凡你想到的不是矢量的物理量，那它就是标量。包括但不限于：路程，速率；功，功率，机械能，势能，动能；密度，温度，质量，体积，面积；电量，电流，电压，电容，电感；磁通量，电通量……

考点：这玩意儿要考就只会考选择判断类的题目，比如随便给你一个东西，问你这个是不是矢量或标量之类的问题。

动量定理

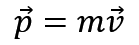
这个公式没什么好说的，经典中的经典。要注意动量是个矢量。

接下来是求质点所受到的合外力公式

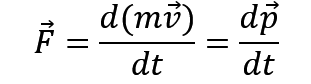
要想理解这个公式首先我们要先知道冲量的公式

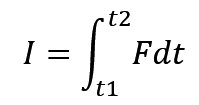
冲量表示的是质点所受合外力在 t 时间内的累积量。同时冲量还是个矢量，于是我们就有这样一个公式

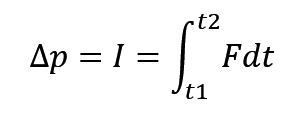
动量差等于冲量，所以当我们对动量关于时间的求导，也就是时间无限接近于零时，就会得到合外力公式。

那反过来，如果已知合外力，求动量，那直接对合外力积分就完事了。

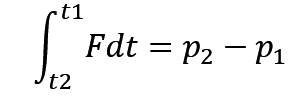
好好好，说了那么多其实也顶不上一句话，求合外力求导动量就完事了，已知合外力求动量，对合外力求积分就完事了，没那么麻烦。

值得注意的是，动量方向和冲量方向并非一致，冲量方向和动量增量的方向一致。

平均冲力：物体与物体之间因碰撞或爆炸等作用时间短，但作用力却很大的力称为冲力。冲力随时间变化大，因此用平均冲力表示

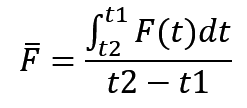
考点：这个我猜测会考的侧重点在于计算，以及不同方向上的动量守恒定理的考察。我们都知道一道题很多时候动量都是在某一个方向上守恒的，所以这类题目会考的多一些。选择题，填空题，大题应该都会出现。

欧头，又到了紧张刺激的测试环节了

答案：

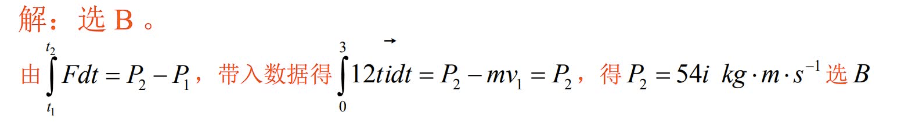
别急还有两题

答案：B

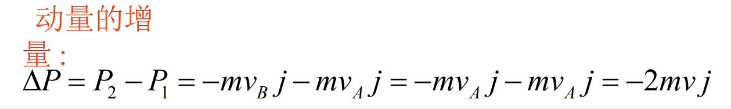
最后一题了哈兄弟们别急

答案：1.25N.s

质点系的动量定理

就一个结论：内力不能改变系统的总动量

动量守恒定律

在碰撞、打击、爆炸等外力可以忽略不计的情况下，系统的总动量可以近似于守恒。

系统内所有之巅的动量都必须对同一个惯性参考系而言。

如果系统的合外力不为零，可能合外力在某一方向上的分量始终为零，则系统在该方向上动量守恒。

质点的角动量

物体在做绕行运动时，动量已不再守恒，于是我们就引入了角动量。也就是说，如果物体做绕行运动，就用角动量定理，不要用动量定理。

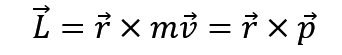
需要注意的是，角动量所用的符号是叉乘，也就是说，如果我们要求角动量的大小的话，就要用到正弦函数。

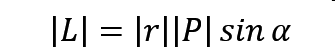
还需要注意的是·，判断角动量的方向，需要用到右手螺旋定则。（具体见课本第四十五页图2-28）

就我的理解来说·，角动量其实就是做圆周运动上的过圆心的轴线罢了，再用右手定则判断出方向即可。

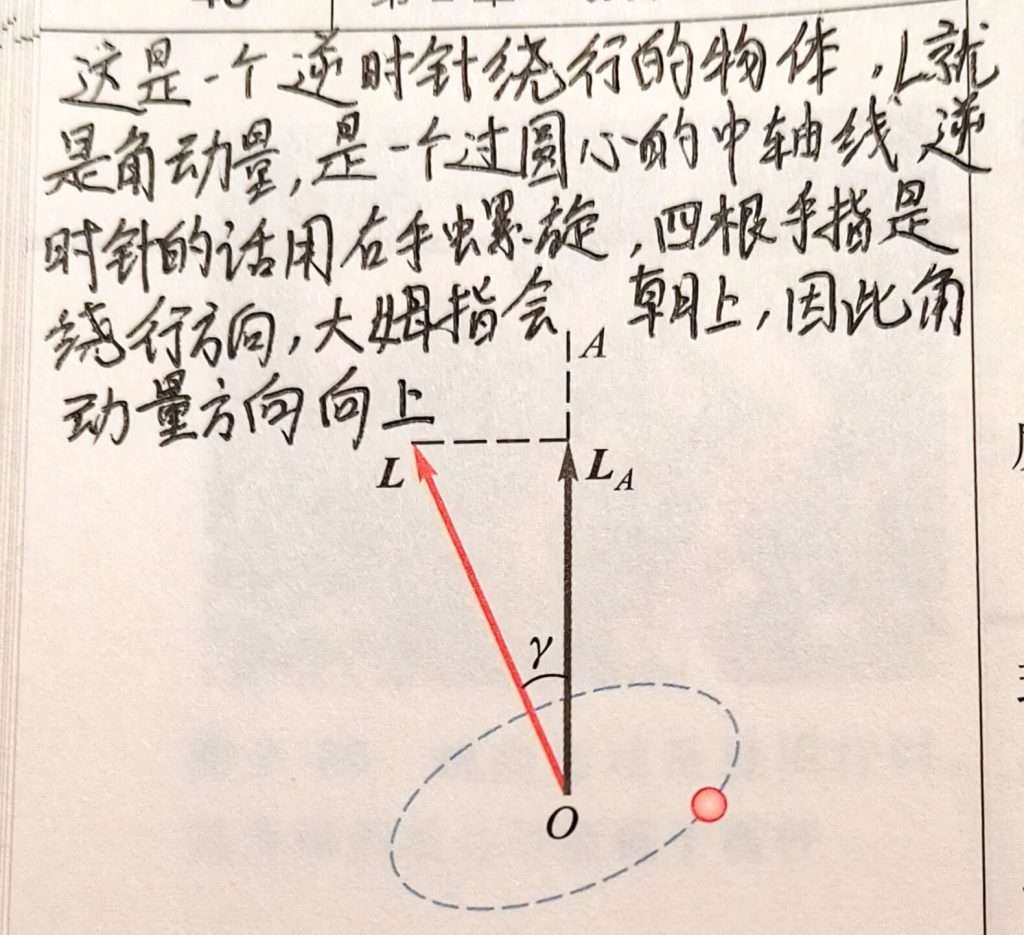
（LA不用去管，角动量关于一个方向上的分量罢了）

值得注意的一个知识点：行星绕日运动、卫星绕行星运动、微观粒子散射运动都角动量守恒。

考点：根据老师的意思来说应该是不怎么考，不过我还是找了道选择题随便做做吧

答案：C

力矩

如果我们对角动量以时间为未知量去求导，就可以得到

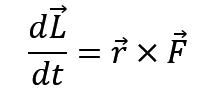
这个公式表示，角动量随时间的变化率不仅和 F 有关，还和位矢 r 有关。我们将这个求导出来的玩意儿叫做力矩，用 M 表示，同时要注意的是，他是矢量。方向垂直于 r 和 F 所构造出来的平面（详见46页图2-31），如果你有看过这张图，并且理解了我上面说的，叉乘是和平面有关的符号，那你就能理解这个方向的含义。

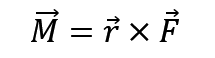
好的我们发现力矩也是叉乘，那大小的求法相信大家也会了，这里就不展示了。（详细见课本第46页）

考点：个人感觉不太可能出这类的题目，因为挺难的这个东西，不过我还是找到了相关的题目，比较简单，纯计算题，有兴趣的可以挑战一下

要做这题得会一个知识点

答案：L=mabwk ；M=0；

能量守恒定律

能量既不能被创造也不能被消灭，只能从一种形式转化为另一种形式，系统各种能量的总和保持不变。

功和功率略解

功

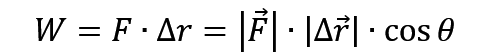
非常非常需要注意的是，做功公式，仅仅适用于恒力，也就是说，如果是变力做功的话，就千万千万不要用这个公式去求功，而应该用动能公式去求做功。

还需要注意的是，以上的公式，只适用于直线运动，但在我们所做的题目中，一般来说，做的都不是直线运动，因此就出现了不是做直线运动式的做功公式

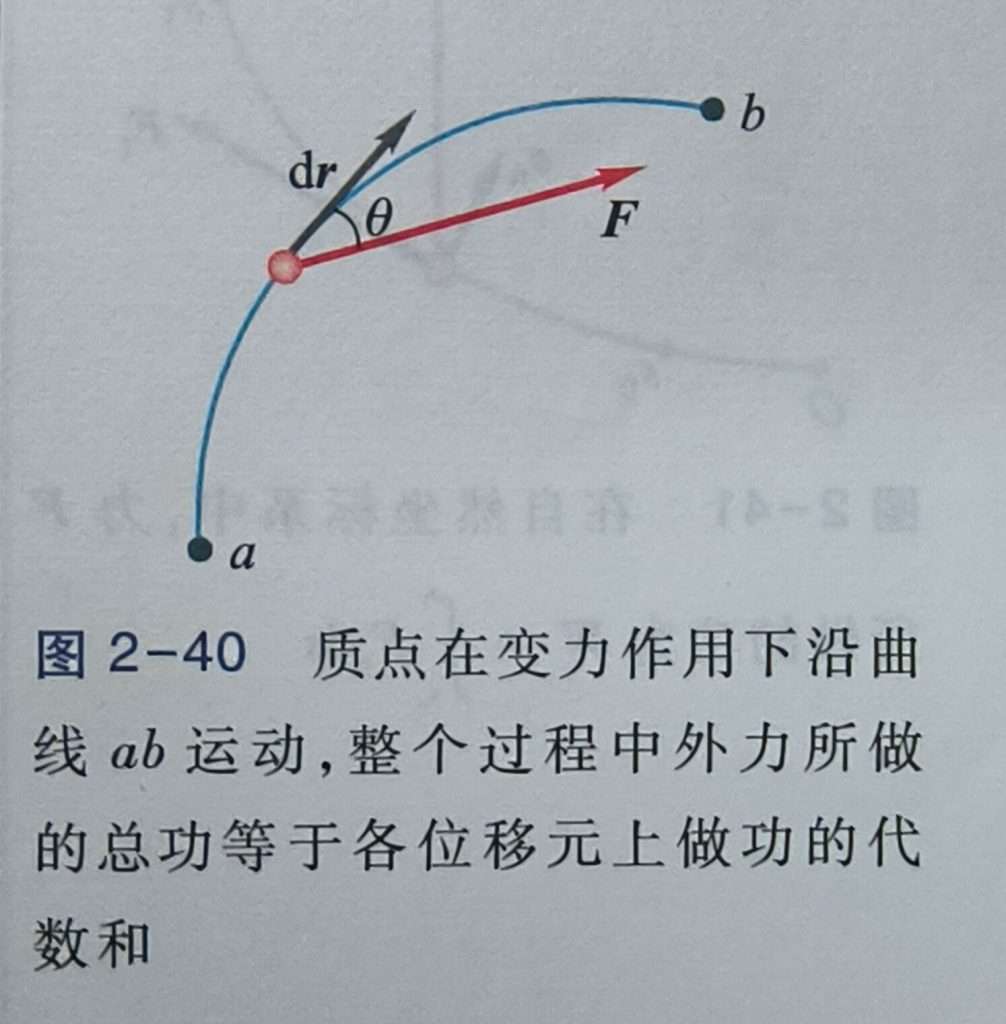
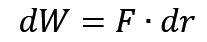
将曲线 ab 看作是由无数微小的位移 r 组合而成，那上面这个公式就是其中一个微小位移所做的功，称为 元功，那你想求一整段曲线 ab 所做的功，就只要对功求在 ab 范围内的积分就可以了。

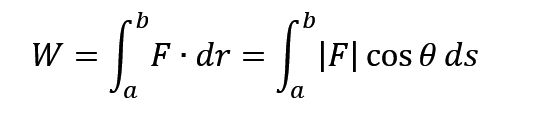
可以看到功是点乘，因此求功的大小时，应该用余弦。

下面我们来看一道题：

这道题可能有点小难，看你能不能想到吧

答案：12J

这道题其实就是求出一个恒力做得功，再用总功减去这个恒力做的功就可以了，不要想复杂了

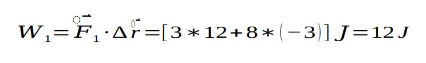
再来一道简单到用脚都能想出来的题目（真的简单吗？）

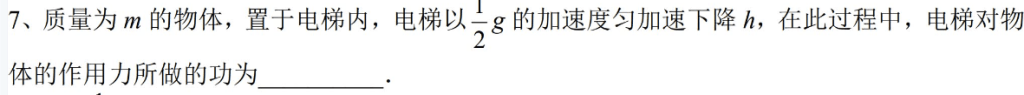
答案：-1/2mgh；让我来看看有几个蠢蛋想的是1/2mgh。

功率

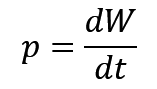
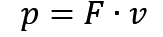
这个两个公式没什么好说的，两个公式直接背就完事了，然后功率是标量。

动能和动能定理

动能定理的话就一个最核心的公式

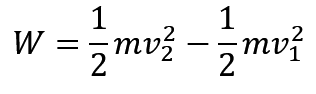
上面也提到了，当物体受到变力而做运动时，做功公式 W=Fs 将不再适用，这个时候，就要用上我们的动能定理。

W>0,物体做正功；W<0物体做负功

注意：（1）功是过程量，动能是状态量；（2）功和动能依赖于惯性系的选取，但对不同惯性系动能定理形式相同。

质点系的动能定理

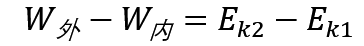
质点系的动能的增量等于作用于系统的所有外力和内力做功的代数和。也就是说，在质点系，内力所做的功，也可以改变系统的动能。但是要注意区别质点系的动量定理，在质点系的动量定理中，内力不能改变动量。

保守力与非保守力

保守力：做功只和始末位置有关跟所经历的路径无关

重力、弹力、电场力、库仑力、万有引力

非保守力：做功不仅取决于始末位置，还和运动路径有关。

摩擦力

考点：我觉得他可能会考一个选择判断类，比如它的一个选项可能会写摩擦力是保守力，或着重力是非保守力都有可能。

势能

因空间位置变化而改变的能量叫作势能，势能的变化只取决于始末位置。

保守力做功等于势能增量的负值。例如一个物体受重力作用下落，重力是保守力且重力做正功，但是势能这个时候是减少的；如果上抛一个物体，重力做负功，但是势能却增加了。

需要注意的四个考点：

一、势能存在于与保守力相关联的整个质点系统，例如重力势能属于物体与地球组成的系统。

二、势能的大小是相对的，且都是状态量；

三、势能具有相对性，势能大小与势能零点的选取有关。

四·、无论零点设在何处，空间任意两点的势能差总是确定的。

下面再给几个求势能的公式：

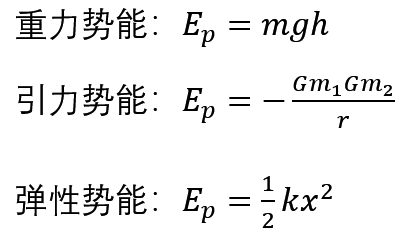
（不会吧不会吧，你不会觉得自己又可以了吧。）

考点：盲猜这个应该会考选择题；下面我们来做几道判断题：

（1）当重力对物体做正功，物体的重力势能可能减小（）

（2）弹性势能是绝对的，而重力势能是相对的（）

（3）势能差与势能零点的选取无关（）

（4）当重力对物体做正功时，重力势能一定减少，动能一定增加（）

答案：（1）错，重力势能一定减小，包反应的老弟；（2）错，势能都是相对的；（3）对；（4）错，比如坐电梯下去。

机械能和机械能守恒定律

首先我们来介绍下什么是机械能，简单你来说就是某一时刻下，动能和势能之和称为机械能

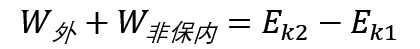
机械能守恒定律：如果系统内只有保守内力做功，其他内力和一切外力都不做功，则系统内各物体的动能和势能可以相互转换，但总机械能保持不变。

注意哈，这里头有个很重要的东西是 系统内，这也是很容易错的一大考点，因为很多题目都很喜欢偷换概念，把系统中的某一个东西单独拎出来讨论他的机械能是否守恒。

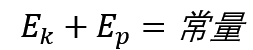
考点：包出选择题跟大题的老弟，选择题出的概率会很大

ok，如果你看到这里觉得你又可以了，不妨来看两道题，包给你打回原形的老弟

（不会有人第一题都不会做吧，不会吧不会吧）

答案：（1）C；（2）C（如果你做错了，那聪明的你自己去作业帮寻找答案吧）

本来到这边就结束的，后来看到了一道比较有意思的题目，给各位加上

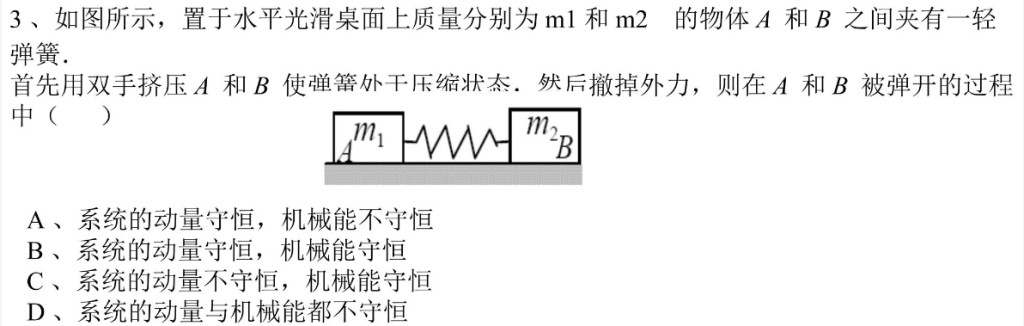
也许你可以很快给出答案，选 A ，但是如何通过以上知识讲述出来才是最关键的，就比如如何用上面的功能定理讲述为什么这道题目的机械能不守恒。

碰撞

如果在碰撞后，两物体的机械能没有任何损失，我们就称这种碰撞为弹性碰撞（或完全弹性碰撞）。

在一般情况下，两物体碰撞时，总要损失一大部分机械能（转变为其他形式的能量，例如放出热量等），这种碰撞就称为非弹性碰撞。

如果两物体在碰撞后，以同一速度运动，并不分开，这种就称为完全非弹性碰撞。
（具体公式看课本60-61页，公式这里就不打了，太长了，手都搓冒烟了）

值得注意的是

在完全弹性碰撞的情况中：动量守恒，机械能守恒。

其余碰撞都为：动量守恒，但机械能不守恒。

这表示在遇到非弹性和我完全非弹性碰撞时，去列动能定理的时候，记得加上损失的能量。

ok，来道很简单的大题试试水，验验你是不是小丑

答案

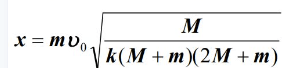
再来一道选择题吧

答案：B；【m2v2sin30=（m1+m2）v】这题考查的就是水平方向上的动量守恒

光看不练怎么行，一起来和物理嗨嗨嗨吧铁子

答案：很简单的问题，自个儿算吧，答案是拿来给你验证的，不是来给让你成为自以为会了的自信小丑

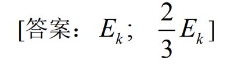
简谐振动

首先直接来说简谐振动最核心的三个公式，要牢牢刻在脑子里

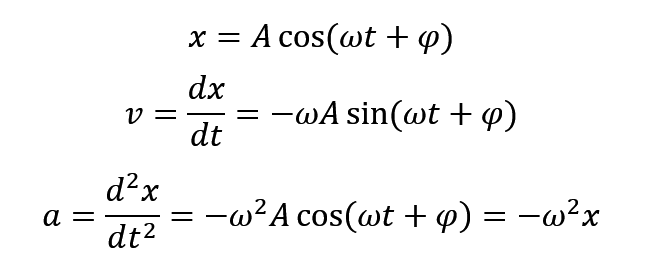
和我们第一章所学的位移公式是一样的转化过程，首先知道 x ，我们就可以通过求导和二次求导得到 v 和 a ，总的来说，如果我们知道了 x ，v ，a 中的·任意一个公式，也可以反推出任意一个物理量。

下面再给大家几个基本的物理量换算，这些都是基础中的基础，一定得记住

接下来再给大家介绍一个很牛逼的东西，叫做简谐运动的旋转矢量

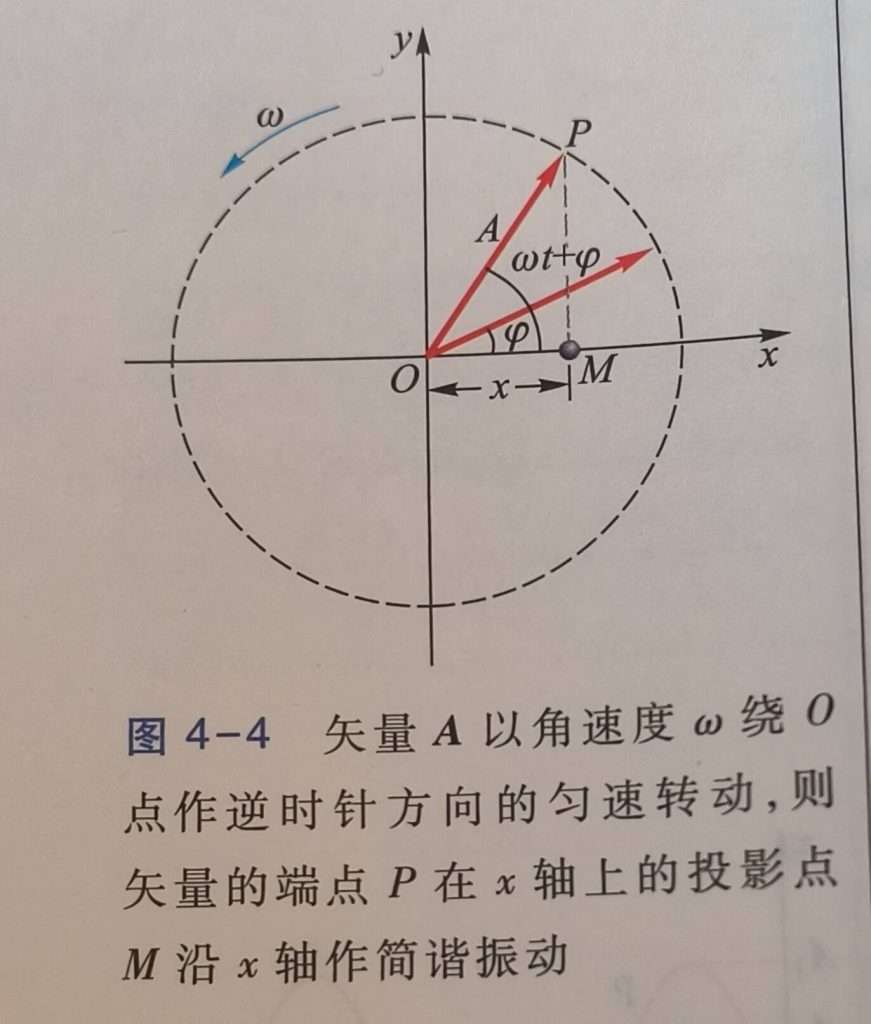
这个东西的牛逼之处在于它可以用图像的思维去理解简谐运动，把上面 x 公式的运动轨迹看作是一个圆，振幅 A 当作了圆的半径，然后 w 看作是角速度，以及初相位和相位用夹角来表示。然后物体的位移就用 x轴上的 OM 表示，OM 其实就是 p 在 x 轴的投影。

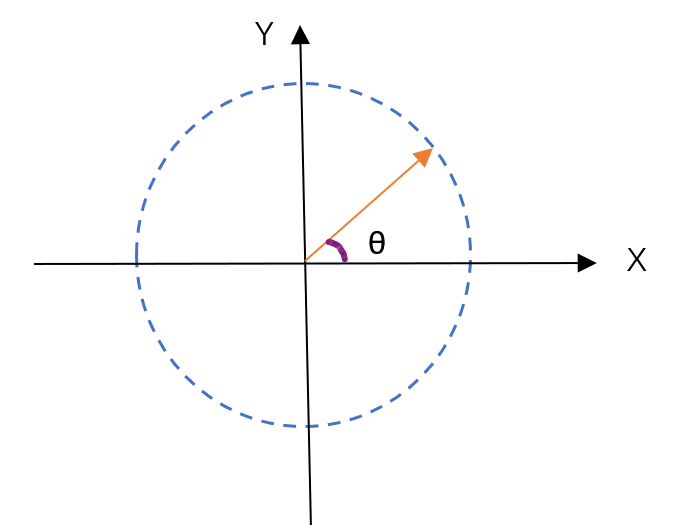
好的首先我们得知道一个规则，那就是简谐振动的旋转矢量始终是沿着逆时针运动的。然后我们再讲一下夹角的规则，当这个向量（红箭头）与 x 轴的夹角在上半部分时，我们的夹角就是正的，也就是说，我们的初相位就是正的。

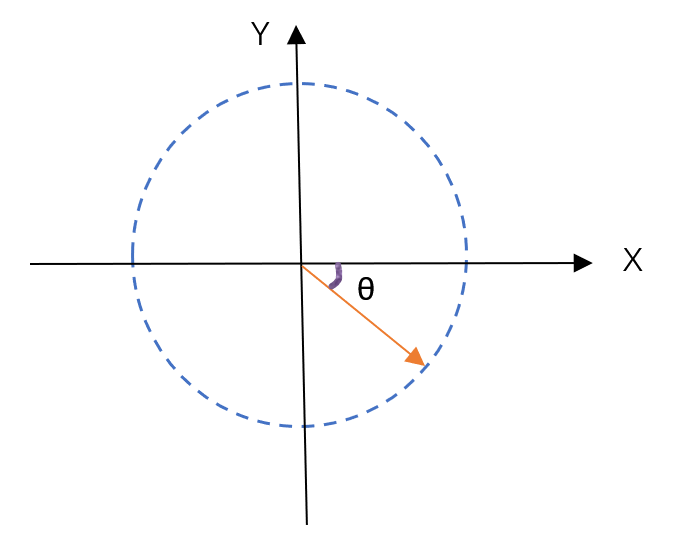
那如果反过来，向量与 x 轴的夹角在下半部分，那夹角就是负的，也就是说初相位就是负的

ok讲的很明白了，因为上面夹角的知识是高中的内容，接下来我们再讲讲位移，所谓位移就是让向量投影在 x 轴上，随着向量逆时针的不断旋转，投影的位置也在 x 轴上不停的移动，移动的这段距离就是物体的位移。

好的讲完了之后我们直接上课本例题实战（详细请看课本117页）

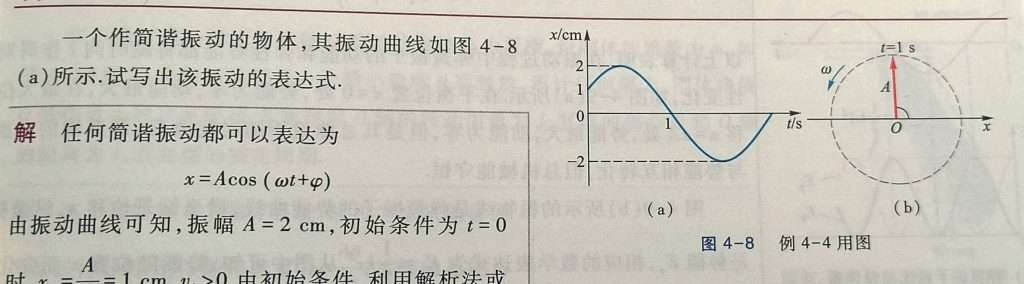
这道题给了我们一个振动曲线图，然后让我们试着写出振动表达式

我们先观察这个振动曲线图，他的振幅 A 是 2 ；然后当 t=1 时，x=0；还有关键的一点是，他刚开始 t=0时 x=1，这说明什么，这说明刚开始的时候，物体的位移是 1 且为正。我们再观察他的走向，是不是先正后负，也就是说，如果用旋转矢量来看的话，也就是图 b ，这个物体先在x轴上正向移动，然后再向负方向运动，然后旋转矢量又是逆时针运动，那你就能猜出初相位了

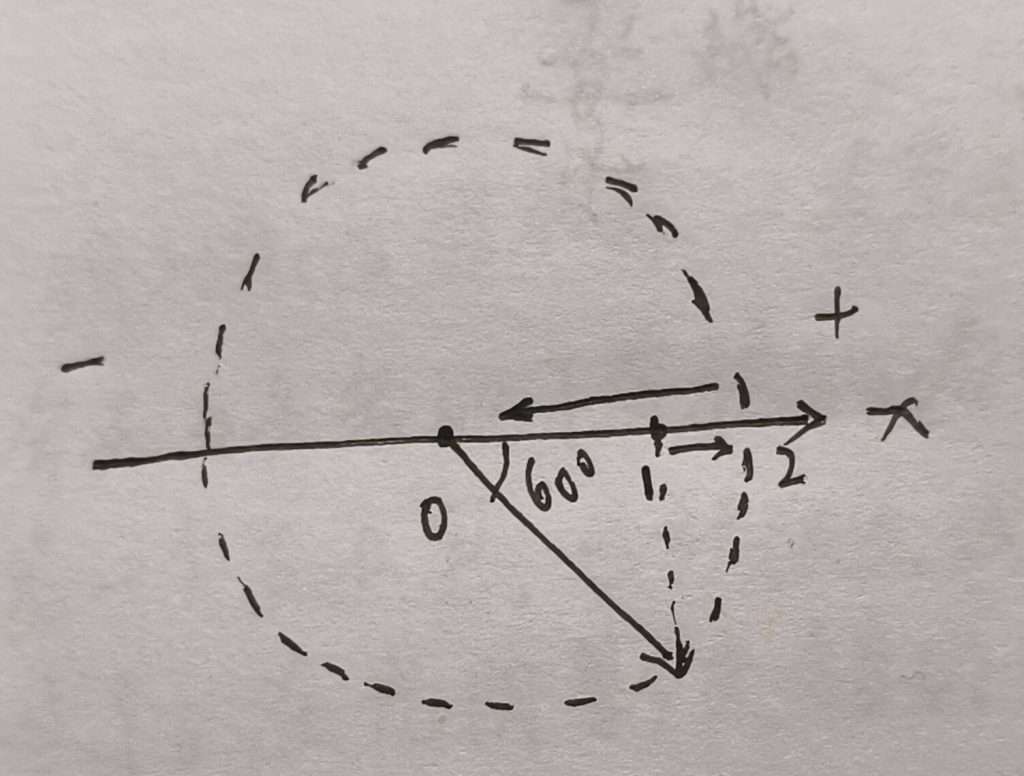
用旋转矢量来表示就长这样，因为在下半部分，那初相位就是负的三分之派，这时候你就可以得到他的振动表达式了

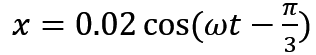
下面我们来看看 t=1 ,x=0 如何使用，其实也是通过旋转矢量，画出一秒时的图案

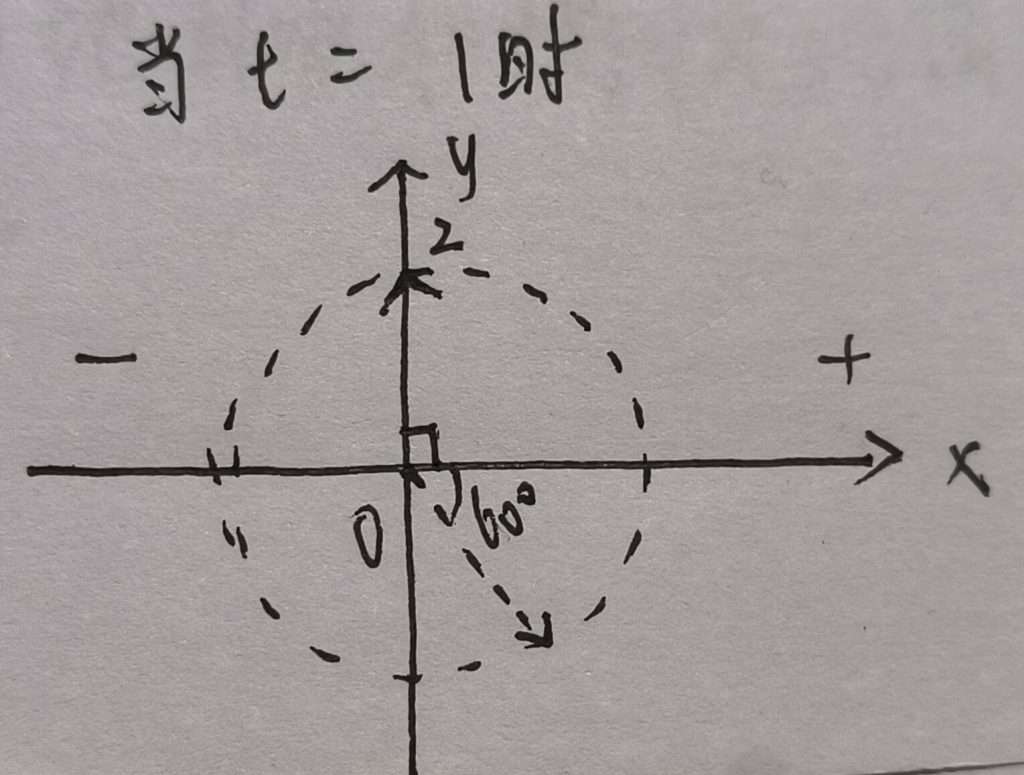
我们可以看到一秒是走了150°，也就是六分之五派，那 w 是不是就有了，ok，那表达式就可以写出来了

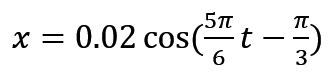
其实这种题目还是有一些小细节的，比如单位的换算，振幅的单位是 米，角频率的单位是 rad/s，做题的时候需要注意。

来吧，上题

答案：

简谐振动的能量

这个能量其实跟求动能和势能的公式没有区别，就只是把 x 和 v 换成了简谐振动的公式而已。

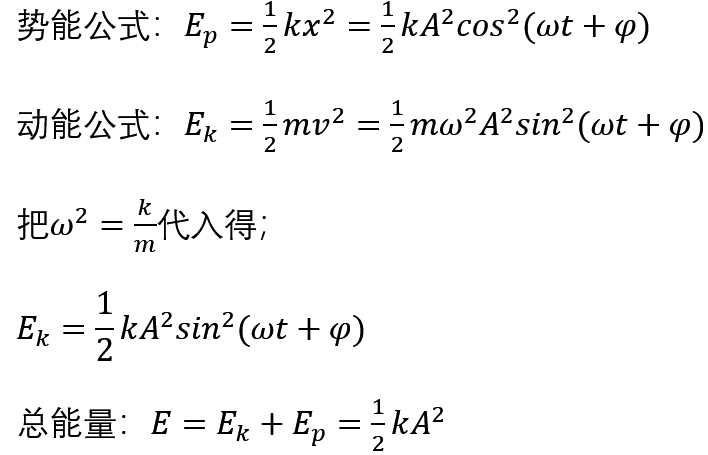
这个公式说明，简谐运动的动能和势能都将随时间而改变，但是系统的总机械能守恒，因为总能量是一个定值。

考点：只能是计算题，这里建议看看课本118页例题4-5，基本上涵盖了所有的知识点

振动的合成

振动的合成需要用图像来分析，所以需要熟悉课本120页图4-11，这张图描述的是两个振动用旋转矢量表示并且合成振动的过程。

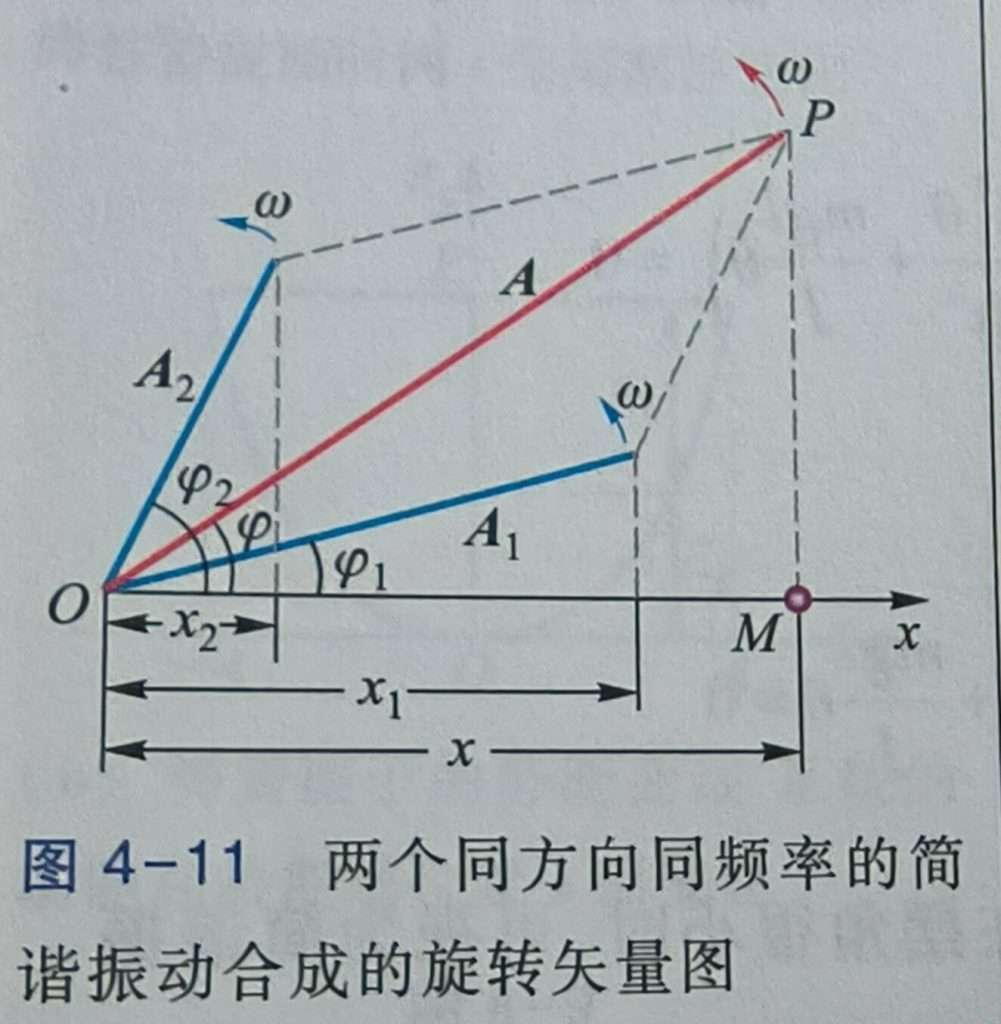
如图中给了我们两个初始简谐振动（蓝色）A1 和 A2，然后我们要求他的合振动，这个时候我们用平行四边形法则，直接画出合成振动（红色）A。用图像的方法可以直观地展示振动的合成过程，接下来我们来讲公式

公式比较复杂，所以兄弟们一定不要乱

我们设初始的两个振动的表达式为 x1 和 x2

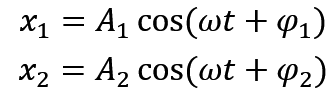
然后我们设合成振动表达式为

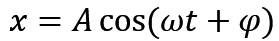
然后我们就可以求合振幅 A，这里用的是余弦公式

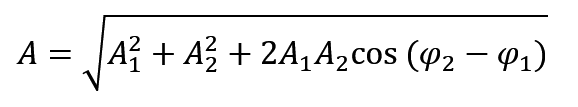
然后如何求初相位呢，这里先将比较麻烦的，课本里的公式法，还是上面的那张图，他就是把两个蓝色向量都投影到 x 轴跟 y 轴上，然后 x 轴上的所有投影相加，y 轴上的所有投影相加，最后直接 y/x 求出初相位的正切值来求初相位。

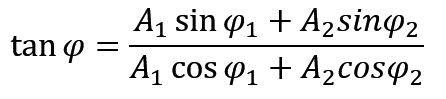
所以看似很长的一个式子其实理解起来并没有那么复杂。

好的接下来我们来讲讲比较简单的，但是仅适用于特殊角度的图像法。（盲猜考试考的两个振动表达式应该都是特殊角度。）

好的我们用课本121页的例题4-7来举例子

题目给了两个振动表达式，我们通过旋转矢量法把两个振动表达式转化成图像，再进行合成，根据平行四边形法则，合矢量的初相位刚好是四分之三派，甚至连合振幅都可以用勾股定理求出来。因此如果拿到一道振动合成类题目，不妨先画个图，看看能不能用旋转矢量法秒杀，如果不行，再用公式去解。

然后就是求最值的问题，题目可能会问你说两个振动合成振幅的最大值和最小值怎么求，这个时候我们还是用上面的课本例题来解释，这就是一个很简单的向量加法问题，你可以把问题转换成，什么时候两个向量相加最大，什么时候两个向量相加最小，那是不是就是两个向量随着时间移动重合的时候，同向重合振幅最大，反向重合振幅最小，因此合振动的最大值就是 A1+A2，最小值就是 A1-A2 。

再讲讲我觉得可能会考的图像题，就是这种图像类的振动合成问题。我们先来说一下振动合成的条件，就是需要同频率。

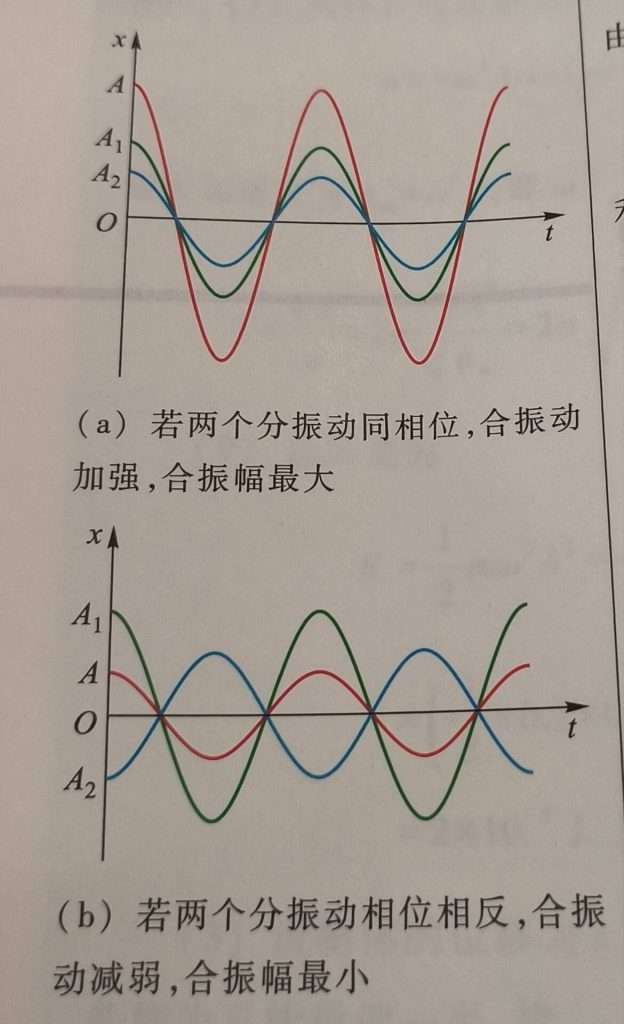
确认是同频率的两个振动后，就看图像嘛，你要是波峰对波峰，波谷对波谷，那就是加强振动，说明这几个振动同相位，也就是说，这几个振动的相位差为

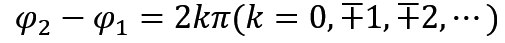
要你求振幅 A 的话直接相加就可以了

如果是减弱振动的话，那就是波峰对波谷（中间会空出一个圆圈型的空白的），这个时候几个振动的相位差就会变成

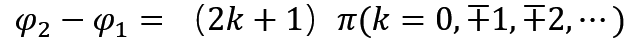
要你求振幅 A 的话直接相减就可以了。

好的直接来放题看你有没有认真看

（这道题要是上面讲了那么多还不会做的话，那你就要拖出去枪毙了）

答案：B ；首先我们审题，虽然给了我们一个振动合成的图像，但是让我们求的啥，合振动的初相位，因此，这道题就得画图来解决，当然你要是很牛逼，可以选择用公式法。

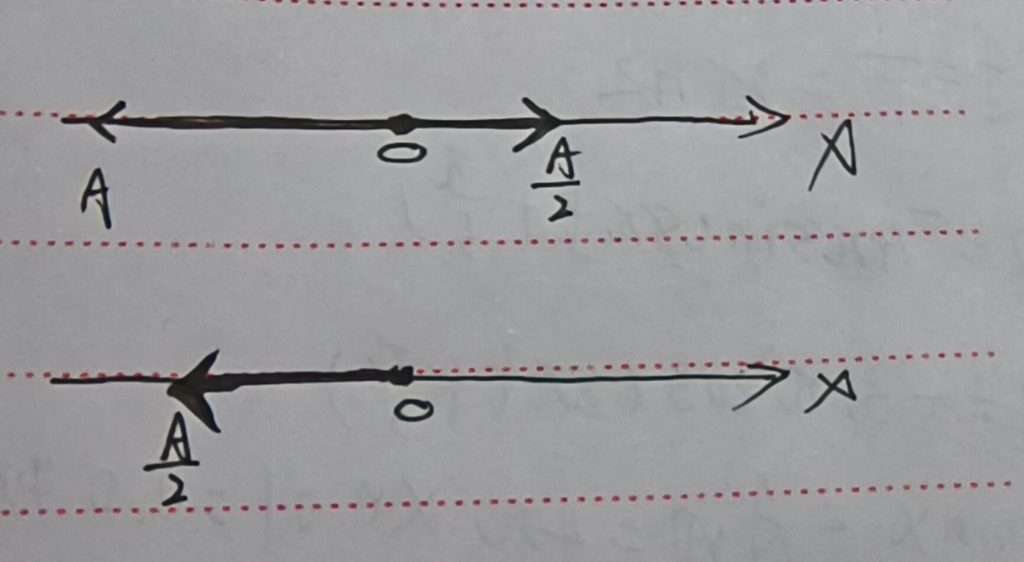
旋转矢量法画出两个振动图像，然后合成，最后只剩下一个在 x 轴上指向负方向的合振动，那合振动的初相位就是向量和 x 轴的夹角，那就是啥，正负派呗。所以这道题融合了上面讲的两大知识点，自个儿研究。

再来一道非常非常容易错的选择题，我猜猜，应该会有百分之九十的人会得出初相位是负的三分之派，然后选不出答案的吧。

答案：C ；解析：很简单的一道题，用旋转矢量就可以判断，唯一的考点在于他的 y 轴是个陷阱，这是振动表达式的速度的图像公式，而不是振动表达式图像。这个时候要怎么办呢，不急，逆推就可以了

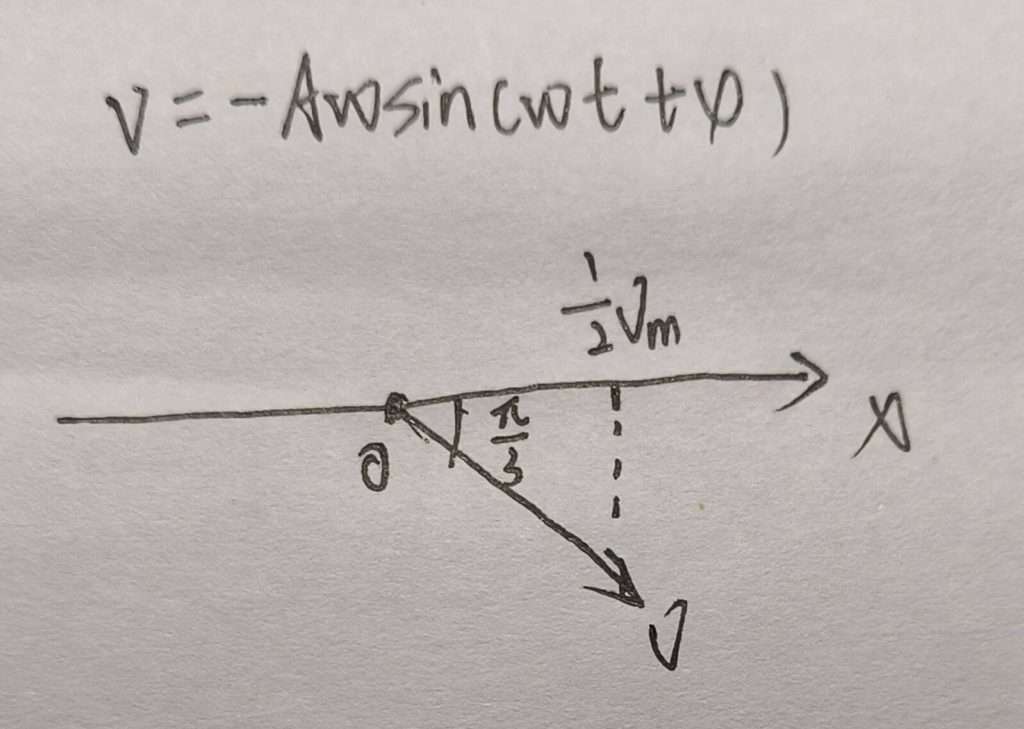
我们首先用旋转矢量来判断速度的初相位，并列出了速度的公式，可是再仔细审题之后会发现，题目要求的是余弦公式，那我们就不得不提到正余弦的转化公式了，知道很多人都忘了，没事我预判到了，直接给你打包好了

然后我们列出转化后的公式

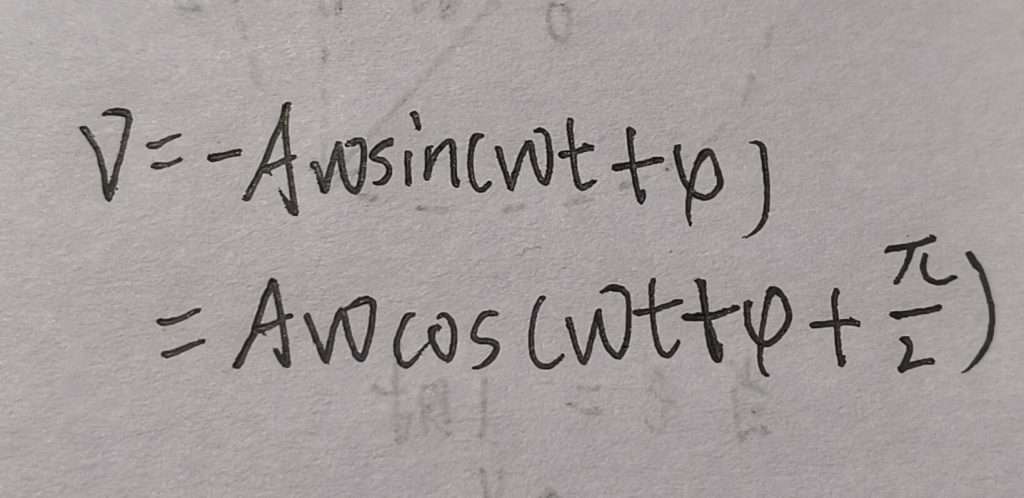
那我们就可以列出等式

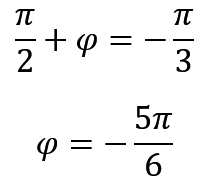
同时我们从这个推导式子中得到一个既定事实，那就是，速度相位比位移相位超前二分之派

机械波的产生和传播

都是知识点，感觉不会考

波的分类，就两种：机械波和电磁波

区别：机械波的传播需要介质，电磁波不需要

常见的机械波：声波、水波、地震波；

常见的电磁波：无线电波、光波、红外线、紫外线、x射线、伽马射线

机械波产生条件：一、有振动源；二、有能够传播机械波的介质

机械波分为两类：横波（P波）和纵波（S波）

水面波是横波和纵波的结合，各质点的轨道近似于圆形

平面简谐波

首先来介绍一下波的一些重要物理量

要理解起来也不复杂，除去频率的话就是路程、速度、时间，OK没了，所以他们的换算公式也是一样的

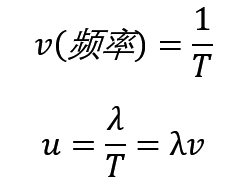
相当于在速度等于路程除以时间的基础上多记一个频率公式就可以了

接下来再说一下重点中的重点，平面简谐波的波动表达式，这是重点中的重点，而且是必考的那种，所以一定要记住表达式

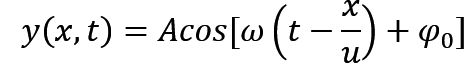
这个公式怎么理解呢，还得从振动公式跟课本的图像来说起

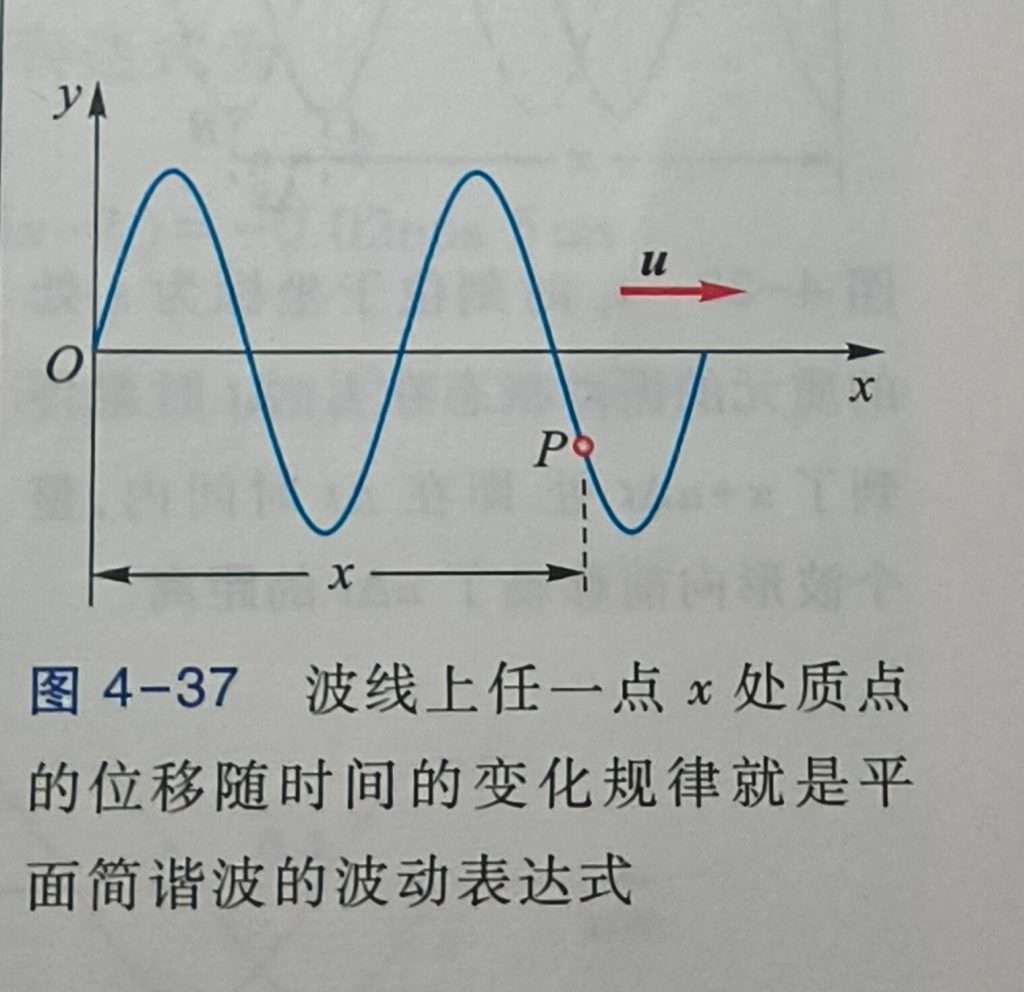
我们会发现说，波动的方程式跟振动的方程式几乎一模一样，为什么呢。抛开波动的能量损失不谈，我们一个质点不管在波的什么位置，是不是其实振动规律都是一样的。对啊，那说实话振动方程式不就是求波从 x=0 时开始振动的公式吗。可我现在振动表达式会了，我感觉自己起飞了，想求一求 p 点的震动表达式，有什么办法，是不是减去从 p 点到 x 点开始振动的时间差就可以了，所以才有了上面的那个公式。

t-x/u 可不就是 t0-t 嘛，这就是波动表达式

然后各种换算自己看课本139页，重要的还有一个

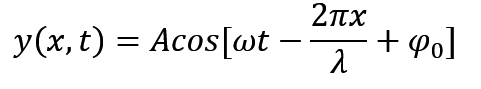
就我给的这两个是最常用的，其他的也就没什么了

考点：这一块肯定就是计算类的问题会特别多，练习的话我建议直接做老师布置的题目，课本的问题考到的知识点就很全面了已经，没有必要再放题了。

总结

这次考试的题型肯定是不会太难的，会停留在知识表面，不会深挖定义，所以只要课本的知识能明白个大概，就不会考得有多差，考试重点肯定是会放在第二单元的运动学，所以这一类的题放的也稍微多一些，题目都是主要集中在选择题和填空题，大题的话直接看老师布置的课本题就行。大家努努力对吧，多刷几道题目，找到做题的手感和规律，期中肯定就能考个理想的成绩。

番外

那我们的期中复习材料到这里就结束了，这一系列的文章是从一个月前开始写的，网站是从上个学期就开始搭了，很多时候也是紧赶慢赶，花了很多的时间和精力去做这个东西。本来平时要上课，我还得一直不断的打比赛，还得出材料，还得挤时间出来去做活动赚谬值，忙爆了。且看且珍惜吧，因为很有可能熬不到期末就被腰斩了，实在是没那么多的精力和时间去接着写复习材料。最开始写这个复习材料也是因为被杰哥训了很久，然后一直在想如何提高大家的成绩，我也就只能想到这样的方法，兄弟就只能帮到这里了，最后预祝各位期中考试旗开得胜。